Teorema de Rolle

 En cálculo diferencial, el teorema de Rolle demuestra la existencia de un punto interior en un intervalo abierto para el cual la derivada de una función derivable se anula cuando el valor que está en los extremos del intervalo es el mismo. Es generalizado mediante el teorema del valor medio, del que este es un caso especial. Es uno de los principales teoremas en cálculo debido a sus aplicaciones.

Fue establecido en 1691 por el matemático francés Michel Rolle (1652-1719).

Se puede enunciar de la siguiente manera,

si ${\displaystyle \ f}$ es una función continua en un intervalo cerrado ${\displaystyle \ [a,b]}$, derivable sobre el intervalo abierto ${\displaystyle \ (a,b)}$ y ${\displaystyle \ f\left(a\right)=f\left(b\right)}$, entonces: Existe al menos un punto ${\displaystyle \ c}$ perteneciente al intervalo ${\displaystyle \ (a,b)}$ tal que ${\displaystyle \ f'(c)=0}$. Demostración[editar] Se sabe que existen tres posibilidades, o bien la función que consideramos es constante, o bien tiene algún punto x donde el valor de la función es mayor o bien este valor es menor que en los extremos. Para el primer caso es trivial que en algún punto la función tiene derivada nula (en la definición de derivada el cociente incremental es cero). Gracias a la continuidad de f, la imagen de [a, b], es un conjunto conexo de R, y por lo tanto es un intervalo, el intervalo imagen. La imagen por una función continua de un conjunto compacto es un conjunto compacto, y por lo tanto el intervalo imagen es cerrado y de longitud finita: es de la forma [m, M], con m el valor mínimo de f y M su valor máximo. Si m = M , la función es constante, y cualquier punto c de (a, b) conviene. Descartado este caso, m ≠ M significa que uno de los dos no es igual a f(a) = f(b). Supongamos que sea M. Entonces M > f(a) = f(b), y por lo tanto el máximo M se alcanza en el interior del intervalo. Sea c en [a, b] tal que f(c) = M. Por definición del máximo, M = f(c) ≥ f(x) para todo x de [a, b]. Entonces el cociente (f(c) - f(x)) / (c - x) es positivo cuando x < c (porque su numerador es siempre positivo y su denominador es positivo no nulo), y es negativo cuando x > c (el denominador se vuelve negativo no nulo). Pero f'(c) es por definición el límite de este cociente cuando x tiende hacia c. El límite por la izquierda, f '(c-), tiene que ser igual al límite por la derecha, f '(c+). Por lo tanto este límite común es nulo, o sea f '(c) = 0. 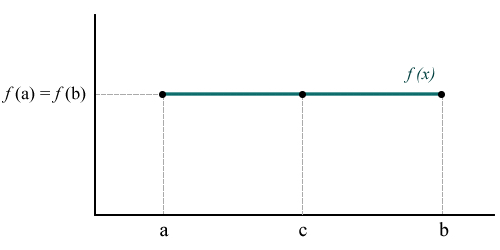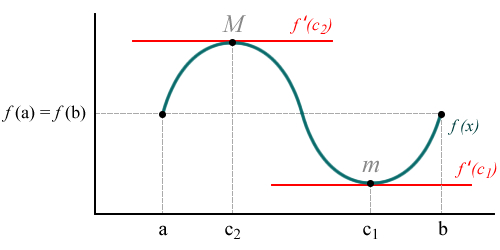La demostración es muy similar si es el mínimo el que se alcanza en (a, b). Demostración gráfica En el siguiente gráfico se observan las tres condiciones: la función es continua en el intervalo cerrado [a,b], es derivable y los valores que toma la función en los puntos a y b son iguales, es decir, f(a) = f(b). Existe, por lo tanto, al menos un punto c que pertenece al intervalo abierto (a,b) en el cual la derivada de la función es igual a cero. Vale observar que c es distinto de a y de b. No debemos confundir c con f(c), que sí puede ser igual a f(a) y f(b). En la ilustración se ve una función constante, pero el teorema no sólo se cumple en este caso. Se pueden dar tres casos en los que f(c) es distinto de f(a) y f(b), a saber: Caso 1. El punto máximo es igual a f(a) y f(b) y el punto mínimo es distinto de ambos, lo cual implica que la curva es convexa. El punto mínimo es m = f(c), y la derivada de la función en este punto es 0. Caso 2. El punto mínimo es igual a f(a) y f(b) y el punto máximo es distinto de ambos, lo cual implica que la curva es cóncava. El punto máximo es M = f(c), y la derivada de la función en este punto es 0. Caso 3. Tanto el punto mínimo como el punto máximo son distintos a f(a) y f(b). Esto significa que dentro del intervalo cerrado [a, b] la función alcanza un punto máximo M = f(c2) mayor al valor de la función en los extremos a y b y un punto mínimo m = f(c1) menor a los mismos. Tanto en el punto máximo como en el punto mínimo, la derivada de la función es nula. Es decir, f '(c1) = 0 y f '(c2) = 0.

Información sacada de:  https://es.wikipedia.org/wiki/Teorema_de_Rolle